leetcode刷题笔记

1.TwoSum

题目描述

题目描述：给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。

示例1：
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1]。

代码详解

解法：代码如下所示，此处展示的方法为哈希表法，相比于暴力双循环法，更快。

主要的思路便是将遍历的数字放入一个map或unordered_map的哈希表中，从哈希表中获取数据速度更快。

class Solution{
public:
    vector<int> twoSum(vector<int>& nums, int target){
        map<int, int> m;
        int n = nums.size();
        int x = 0;      
        for(int i = 0; i < n; i++){
            x = target - nums[i];
            if(m.count(x) == 0){
                m.insert(make_pair(nums[i], i));    //第一次出现的值，放入map中
            }
            else if(m.count(x) && i != m[x]){
                return {m[x], i};           //当map中有与之和为target的值时，输出结果
            }
        }
        return {};
    }
};

注意点

1. 将数值插入map利用的是

   m.insert(make_pair(nums[i], i));

2. 判断某个元素 x 是否存在于哈希表中利用的是

   if(m.count(x)) //m.count(x)的返回值为元素x在容器m中出现的次数。

=========================================================================

2.AddTwoNummbers

题目描述

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。
请你将两个数相加，并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例1：
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例2：
输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

代码详解

大概能想到两种思路

1. 获取每个链表的数字，数字相加，再将结果放入链表中。但这种方式时间复杂度较高。
2. 每一位的数字相加，如果有进位，利用carry记录进位。这方方式时间复杂度低。

详细代码如下

//链表结点的声明方式
struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

class Solution{
public:
    /*思路：和我们进行加法计算的思路相同，利用进位carry，计算每个位相加的值
    */
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2){
        ListNode *head = nullptr;
        ListNode *tail = nullptr;   //作为结果的返回链表的头部和尾部
        int carry = 0;              //作为进位值
        while(l1 || l2){            //当l1，l2其中一个不为空时，就进行计算
            int n1 = (l1 ? l1->val : 0);    //如果l1节点不为空，获取其val值，为空时，值为0；
            int n2 = (l2 ? l2->val : 0);
            int sum = n1 + n2 + carry;
            if(!head){      //插入第一个值的情况
                head = tail = new ListNode(sum % 10);
            }
            else{
                tail->next = new ListNode(sum % 10);
                tail = tail->next;      //将新值插入尾节点，之后更新尾节点
            }
            carry = sum / 10;
            if(l1){
                l1 = l1->next;
            }
            if(l2){
                l2 = l2->next;
            }
        }
        if(carry > 0){
            tail->next = new ListNode(carry);
            tail = tail->next;      //此时不更新尾节点也可以
        }
        return head;
    }
};

注意点

1. 链表节点声明方式如下

   struct ListNode {
       int val;
       ListNode *next;
       ListNode() : val(0), next(nullptr) {}
       ListNode(int x) : val(x), next(nullptr) {}
       ListNode(int x, ListNode *next) : val(x), next(next) {}
   };

2. 注意链表的用法，如何新加节点，如何获取结点的值，以及如何通过前一个结点，进入到下一个结点。

=========================================================================

3.LengthOfLongestSubstring

题目描述

找到字符串中最长的不重复的子字符串。
给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

代码详解

寻找字符串中的子串，想到滑动窗口的方法
又因为强调的是无重复，所以想到hashmap的方法进行优化
详细的代码如下

int lenghtOfLongestSubstring(stirng s){
    //记录最长子串的长度
    int ans = 0;
    int start = 0;  //记录滑动窗口的起始位置
    int end = 0     //记录滑动窗口的末尾位置
    map<char, int> mp;  //hashmap记录字符(char)的位置(int)

    for(int i = 0; i < s.length(); i++){
        //当前遍历的字符没有出现过时
        if(!mp.count(s[i])){
            //首先记录字符的位置
            mp.insert(make_pair(s[i], i + 1));
        }
        //当map中出现遍历到的字符时
        else{
            //判断重复的字符是否在当前的窗口中，如果在则更新窗口起始位置
            start = (mp[s[i]]> start) ? mp[s[i]] : start;
            //更新hashmap中，字符的最新位置
            mp[s[i]] = i + 1;
        }
        //更新滑动窗口末尾的位置
        end = i + 1;
        ans = (ans > end - start) ? ans : (end - start);
    }
    return ans;
}

注意点

1. 记录字符的位置时，使用了，如下代码。这里记录的位置是 i+1 这样方便了后续的比较，更加贴合实际，实际的窗口起始边界一定是在窗口内第一个元素的左边。这样写极大的方便了后续计算长度的操作。

   mp.insert(make_pair(s[i], i + 1));

2. 向map数据结构中插入数值时，使用make_pair(a, b)的写法。

=========================================================================

4.findMedianSortedArrays

题目描述

找到两个排序数组的中位数
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

代码详解

能想到的方法有两种
一：暴力排序，使用一个set容器，将数据排序，然后从新求出中位数，但是时间复杂度过高，不符合要求(具体代码实现如下)。

double findMedianSortedArray1(vector<int>& num1, vector<int>& num2){
            //方法一暴力排序，使用multiset容器，将数据排序，然后求中位数。
        multiset<int> ms;
        for(int i = 0; i < num1.size(); i++){
            ms.insert(num1[i]);                 //将num1中的数据放入multiset容器
        }
        for(int i = 0; i < num2.size(); i++){
            ms.insert(num2[i]);                 //将num2中的数据放入multiset容器
        }
        vector<int> v;                          //利用vector容器复制multiset容器中的数据（为了更方便的遍历排好序的数据）
        for(set<int>::iterator it = ms.begin(); it != ms.end(); it++){
            cout << *it << endl;
            v.push_back(*it);
        }
        int nums = ms.size();                   //获取multiset容器中元素的个数
        if(nums % 2 == 1){
            return v[nums/2];                   //个数为奇数时，返回的中位数
        }
        return (double)(v[nums/2] + v[nums/2 - 1]) / 2;     //个数为偶数时，返回的中位数
    }

二：二分法查找，由于两个数组长度已知，所以中位数在两个数组中的位置可以算出的。只需要维护两个指针，每次将较小的指针向后移动，直到一个指针到达中位数的位置。(代码实现如下)。
这个算法的主要思路：在两个有序数组中找到第K个元素，就可以通过比较两个数组中元素的大小，每次比较将其中一个较小的数组的指针后移，计数器加1，直到计数器的值 = K - 1时，此时中位数就是两个指针指向的较小值。
优化：虽然这个思路很好理解，但是依然有优化的空间，即直接从两个数组的[k/2 - 1]处的值开始比较，这样能极大的加快运行速度。优化的算法有一点绕，可以结合代码进行理解。实在不行就结合题解的图，进行理解。

int getKthElement(vector<int>& nums1, vector<int>& nums2, int k){
        /* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
         * 这里的 "/" 表示整除
         * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
         * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
         * 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
         * 这样 pivot 本身最大也只能是第 k-1 小的元素
         * 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组
         * 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组
         * 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数
         */
        int m = nums1.size();
        int n = nums2.size();
        int index1 = 0;         //数组1中删除的元素的个数
        int index2 = 0;         //数组2中删除的元素的个数

        while(true){
            if(index1 == m){
                return nums2[index2 + k - 1];   //当其中一个数组到达边界值时，可以直接返回中位数
            }
            if(index2 == n){
                return nums1[index1 + k - 1];   //同上
            }
            if(k == 1){
                return min(nums1[index1], nums2[index2]);   //当k值变化到1时，比较此时两个数组中更新后的值的大小，小的一方为中位数
            }

            int newIndex1 = min(index1 + k / 2 - 1, m - 1);  //获取num1中需要进行比较的下标的值（跟m-1比较是为了防止越界）
            int newIndex2 = min(index2 + k / 2 - 1, n - 1);  //获取num2中需要进行比较的下标的值

            int pivot1 = nums1[newIndex1];          //获取nums1中需要进行比较的值
            int pivot2 = nums2[newIndex2];          //获取nums2中需要进行比较的值

            if(pivot1 <= pivot2){
                k -= newIndex1 - index1 + 1;             //更新k值，从寻找第k小的数，更新为寻找第（k - 本次循环删除元素的个数）小的数
                index1 = newIndex1 + 1;                  //删除的个数为下标值 + 1
            }
            else{
                k -= newIndex2 - index2 + 1;             //更新k值，从寻找第k小的数，更新为寻找第（k - 本次循环删除元素的个数）小的数
                index2 = newIndex2 + 1;                  //删除的个数为下标值 + 1
            }

        }
    }

    double findMedianSortedArray2(vector<int>& nums1, vector<int>& nums2){
        int totalLength = nums1.size() + nums2.size();
        if(totalLength % 2 == 1){
            return getKthElement(nums1, nums2, (totalLength / 2 + 1));
        }
        else{
            return (getKthElement(nums1, nums2, (totalLength / 2)) + getKthElement(nums1, nums2, (totalLength / 2 + 1))) / 2.0;
            //偶数个元素时，需要 /2.0 将int型转化成double型，或者使用(double)强制类型转换。
        }
    }

注意点

1. 在寻找第 k 小的数时，在getKthElement()中，利用Index1，Index2两个变量记录已经删去的元素的个数，用newIndex1，newIndex2记录本次循环后，新的删去元素的个数。因此，每次循环之后都要更新index的值，以及更新K的值（这里K代表的是当前数组中第K小的值，由于不断删除中位数左侧的值，所以K的值也要不断减小）

   if(pivot1 <= pivot2){
       k -= newIndex1 - index1 + 1;  //更新k值，从寻找第k小的数，更新为寻找第（k - 本次循环删除元素的个数）小的数
       index1 = newIndex1 + 1;       //删除的个数为下标值 + 1
   }
   else{
       k -= newIndex2 - index2 + 1;  //更新k值，从寻找第k小的数，更新为寻找第（k - 本次循环删除元素的个数）小的数
       index2 = newIndex2 + 1;       //删除的个数为下标值 + 1
   }

2. 注意循环的停止条件，当K=1时，可以停止。当其中一个数组全部删除时，可以停止。

   if(index1 == m){
       return nums2[index2 + k - 1];   //当其中一个数组到达边界值时，可以直接返回中位数
   }
   if(index2 == n){
       return nums1[index1 + k - 1];   //同上
   }
   if(k == 1){
       return min(nums1[index1], nums2[index2]);   
       //当k值变化到1时，比较此时两个数组中更新后的值的大小，小的一方为中位数
   }

3. 最后，当两个数组元素的个数为偶数时，在平均值计算时，需要 / 2.0 将结果转化为double型。

   return (getKthElement(nums1, nums2, n / 2) + getKthElement(nums1, nums2, n / 2 + 1)) / 2.0;

=========================================================================

5.longestPalindrome

题目描述

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = “babad”
输出：”bab”
解释：”aba” 同样是符合题意的答案。

示例 2：

输入：s = “cbbd”
输出：”bb”

代码详解

关于回文串的问题，有许多方法，在这儿先介绍这题的其中一个方法，叫做中心扩展算法。这种方法用时短，内存占用少，比较推荐。
中心扩展算法的本质即使，枚举所有回文中心，并尝试扩展，直到无法继续扩展为止。在枚举过程中记录长度的最大值和最大值时的回文中心。这样我们首先需要一个函数计算一个回文中心的回文串长度，通过比较长度，找出最长的回文串。因为回文串有单数和偶数两种，所以设置了两个回文中心值，单数时让左右值相等即可

int expandAroundCenter(const string& s, int left, int right){
    //计算能扩展出的最大长度
    while(left >= 0 && right < s.size() && s[left] == s[right]){
        left--;     
        right++;
    }
    return right - left - 1;    //注意，当不能扩展时，此时的s[left] != s[right]
                                //返回的回文数长度应该为 (right - 1) - (left + 1) + 1
}

寻找最长回文串的代码如下

string longestPalindrome2(string s){
    int begin = 0;  //记录回文串起始的下标
    int maxLength = 0； //记录最长的长度

    for(int i = 0; i < s.length(); i++){
        int l1 = expandAroundCenter(s, i, i);
        int l2 = expandAroundCenter(s, i, i + 1);
        //分别获取奇数回文串长度和偶数回文串长度
        int l = max(l1, l2);    //记录较长的回文串长度
        if(l > maxlength){
            maxlength = l;  //更新最长子串的长度
            if(l1 = l){     //如果是奇数回文串,记录回文串的起始位置
                begin = i - l/2;
            }
            else{           //如果是偶数回文串,记录回文串的起始位置
                begin = i - l/2 + 1;
            }
        }
    }
    return s.substr(begin, maxLength);
}

注意点

1. 在枚举回文中心时，要同时考虑到奇数和偶数回文串的情况，因此计算了两个回文串的长度，并记录了最长的情况。

   int l1 = expandAroundCenter(s, i, i);
   int l2 = expandAroundCenter(s, i, i + 1);
   int l = max(l1, l2);

2. 奇数回文串和偶数回文串，在计算其实位置时，稍有不同，需要注意。

   begin = i - l/2;    //奇数
   begin = i - l/2 + 1;//偶数

=========================================================================

7.reverse

题目描述

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−2^31,  2^31 − 1] ，就返回 0。
假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

输入：x = 123
输出：321

示例 3：

输入：x = 120
输出：21

代码详解

这是一道比较经典的数字翻转问题，可以利用纯数组的方式弹出和推入数字。

//弹出X末尾的数字，用digit接收。
digit = x % 10;
x /= 10;

//将数字digit推入到输出值的末尾
rev = rev * 10 + digit; 

上面的代码就是将末尾数字取出，并推入到输出值的末尾的方式，这样不仅快，而且节省空间。

整体代码如下

int reverse(int x){
    int rev = 0;
    while(x != 0){
        //每次循环都要先判断是否会出现超出范围的可能
        if(rev < INT_MIN / 10 || rev > INT_MAX / 10){
            return 0;
        }
        int digit = x % 10;
        x /= 10;

        rev = rev * 10 + digit;
    }
    return rev;
}

注意点

1. 由于环境中不允许64位的数据出现，所以在判断是否超出范围时，由于rev不可能小于INT_MIN，不可能大于INT_MAX，所以选择将在更新rev之前，比较rev和INT_MIN / 10，或rev和INT_MAX / 10的大小。

   if(rev < INT_MIN / 10 || rev > INT_MAX / 10)

=========================================================================

8.myAtoi(字符串转换整数)

题目描述

手动实现C++库中的atoi函数，将传入的字符串中的数字提取出来。

1. 读入字符串并丢弃无用的前导空格。
2. 读入下一个字符，直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
3. 读取数字之前的正负号，负号为负。
4. 如果整数超过32位有符号整数，需要截断这个这个数

代码详解

方法一：根据题意解题

明确转化规则

1. 空格处理（一般要跳过）
2. 正负号的处理
3. 数字的处理
4. 注意溢出
   详细代码如下

   int myAtoi(string s){
       int res = 0;
       int sign = 1;
       int i = 0;
       while(s[i] == ' '){
           i++;    //当遇到空格时，跳过
       }
       if(s[i] == '-'){
           sign = -1;
           i++;
       }
       else if(s[i] == '+'){
           sign = 1;
           i++;
       }
       while(i < s.length() && isdigit(s[i])){
           int n = s[i] - '0';
           //注意这里的判断是否溢出的逻辑
           if(res > INT_MAX / 10 || (res == INT_MAX / 10 && n > 7)){
               return sign > 0 ? INT_MAX : INT_MIN;
           }
           res = res * 10 + n;
           i++;
       }
       return sign * res;
   }

   注意：
5. 明确转化时的规则，理清规则后，代码更容易编写。
6. 这道题中，判断是否溢出的逻辑与第7题的有不同，第七题中由于输入值就不会超过32位整数的范围，所以可以通过第7题的判断逻辑，判断是否溢出。但这道题中输入值有超过32位整数范围的可能性，判断逻辑就要发生变化。注意INT_MAX = 2147483647,INT_MIN = -INT_MAX - 1 = -2147483648。这时的判断逻辑写法如下。

   if(res > INT_MAX / 10 || (res == INT_MAX / 10 && n > 7)){}

方法二：自动机

这个题不难，但是为了防止写出臃肿的代码，比较好的方法是使用自动机的概念。即程序在每个时刻都有一个状态，这个状态记为a，从字符串中输出一个字符c，根据c转移到下一个状态a1。图示如下。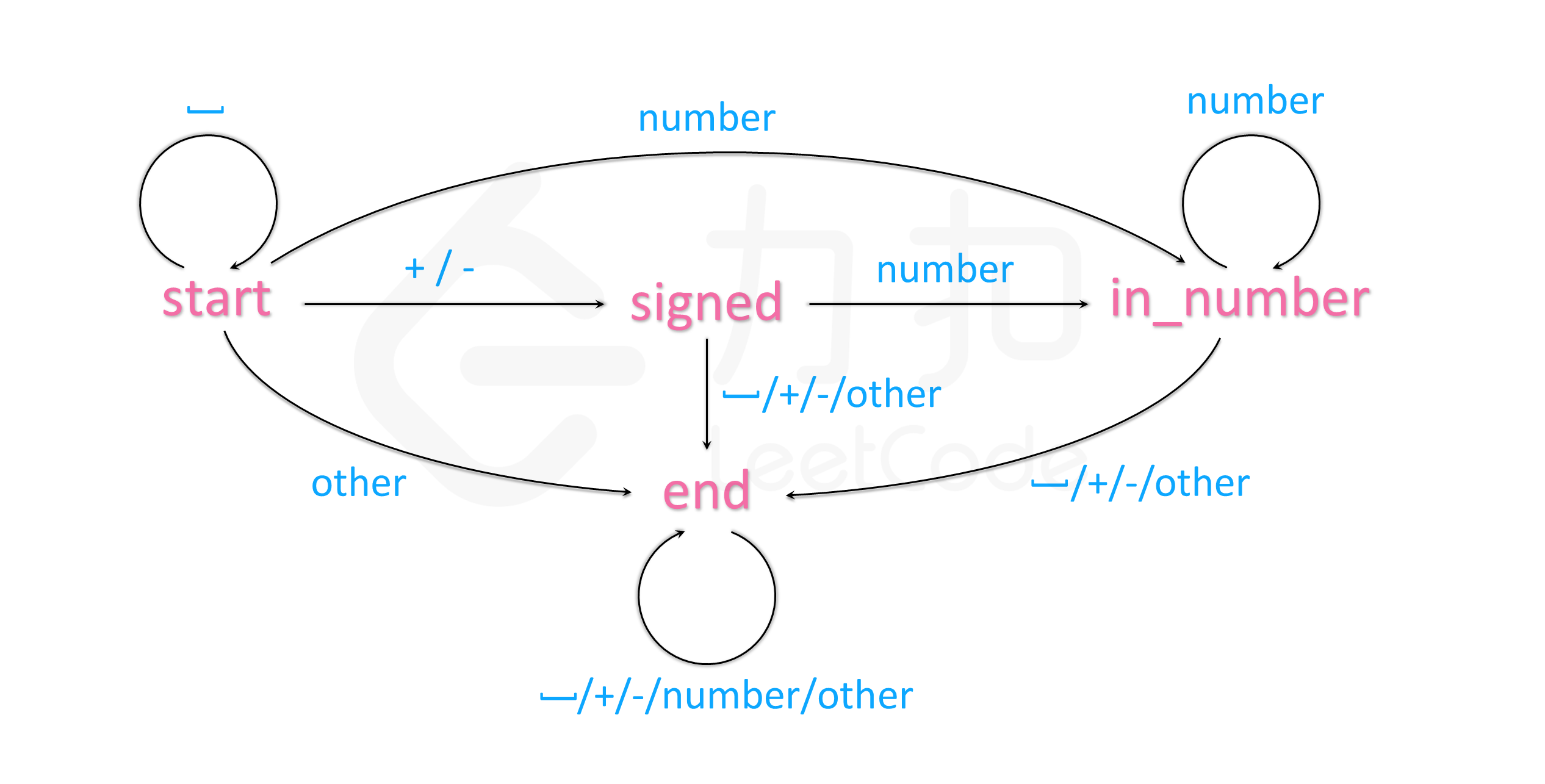

当前状态有四种，分别是“start”，“signed”，“in_number”，“end”。根据当前状态，和下一个读入的字符，可以获取下一阶段的状态。
比如当前状态是“start”，下一个读取的字符有四种可能，空格“ ”，正负号“+-”，数字“in_number”，其他字符“other”，这四种可能的字符，分别对应了下一阶段的状态，即下表中对应的四种状态。再比如当前状态为数字“in_number”，那么根据下一个读入的字符，对应的下一阶段的状态只有两种，当下一个字符是空格“ ”，正负号“+-”或其他“other”时，下一阶段的状态为“end”，即结束状态，只有当下一个字符也是数字“in_number”时，才会继续进行程序。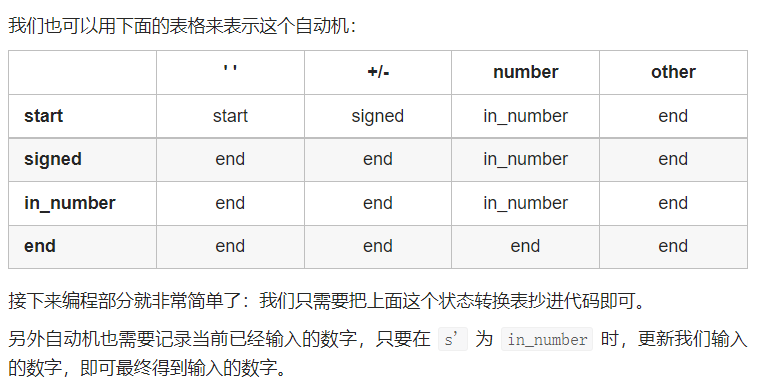

自动机实现代码如下。

//首先创建一个自动机类
class Automaton{
    string state = "start";     //设定初始状态为“start”。
    map<string, vector<string>> table = {//将上图中的表格抄写下来。
        {"start", {"start", "signed", "in_number", "end"}},
        {"signed", {"end", "end", "in_number", "end"}},
        {"in_number", {"end", "end", "in_number", "end"}},
        {"end", {"end", "end", "end", "end"}}
    };

    int get_col(char c){     //状态转移，获取字符，转移状态。
        if(isspace(c)){
            return 0;
        }
        else if(c == '+' || c == '-'){
            return 1;
        }
        else if(isdigit(c)){
            return 2;
        }
        else{
            return 3;
        }
    }
public:
    int sign = 1;
    long ans = 0;
    void getNumber(char c){
        state = table[state][get_col(c)];   //获取当前的状态；
        if(state == "in_number"){
            ans = ans * 10 + c - '0';
            //判断是否溢出
            ans = sign == 1 ? min(ans , (long)INT_MAX) : min(ans, -(long)INT_MIN);
        }
        else if(state == "signed"){
            sign = c == '+' ? 1 : -1;
        }
        
    }
};

class Solution{
public:
    int myAtoi(string s){
        int sign = 1;
        long ans = 0;
        Automaton automaton;
        for(char ch : s){
            automaton.getNumber(ch);
        }
        return automaton.sign * automaton.ans;
    }
};

这两种方法都需要了解，相比之下，自动机写出的代码比较简洁，但是只要思路清晰，第一种方法有很大的优势，写出来的代码也同样可以很简洁。

注意点

1. 要注意理解自动机的概念，在具体的使用过程中，需要结合实际情况进行代码方面的修改。
2. 注意这两种代码中，判断是否溢出的方法。第一种判断方法使用的是int型数据的判断逻辑；第二种方法用的是long型数据的判断逻辑。两种判断逻辑在写法上有不同，需要注意。方法一中，都是int型数据，所以在判断时，用INT_MAX / 10，以及最后的个位数是否大于7，来判断最终的结果是否溢出。方法二中的ans为long型整数，所以判断时，选择将INT_MAX，INT_MIN转换成long型，再进行判断。

   //方法一：
   if(res > INT_MAX / 10 || (res == INT_MAX / 10 && n > 7)){
       return sign > 0 ? INT_MAX : INT_MIN;
   }

   //方法二：
   if(sign == 1){
       //ans为long型整数
       ans = min(ans, (long)INT_MAX);
   }
   else{
       ans = min(ans, -(long)INT_MIN);
   }

=========================================================================

9.isPalindrome(回文数)

题目描述

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false。
回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

示例 1：

输入：x = -121
输出：false
解释：从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

示例 2：

输入：x = 10
输出：false
解释：从右向左读, 为 01 。因此它不是一个回文数。

代码详解

这道题比较基础，写法与之前的将一个数字翻转几乎相同，这里给出时间复杂度最小的一种写法，因为是判断回文数，所以只需要翻转一半的数字即可

bool isPalindrome(int x){
    //首先判断是否是负数，以及个位数是否为0
    if(x < 0 || (x % 10 == 0 && x != 0){
        return false;
    }
    int reverseNum = 0;
    while(x > reverseNum){
        reverseNum = reverseNum * 10 + x % 10;
        x /= 10;
    }
    return reverseNum == x || reverseNum / 10 == x;
}

注意点

1. 对于121型回文数，会出现reverseNum = 12，x = 1的情况，这时，reverseNum / 10 == x即可。

=========================================================================

10.isMatch（正则表达式匹配）

题目描述

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘‘ 的正则表达式匹配。
‘.’ 匹配任意单个字符
‘‘ 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。
示例 1：

输入：s = “aa”, p = “a”
输出：false
解释：”a” 无法匹配 “aa” 整个字符串。

示例 2:

输入：s = “aa”, p = “a*”
输出：true
解释：因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此，字符串 “aa” 可被视为 ‘a’ 重复了一次。

示例 3：

输入：s = “ab”, p = “.“
输出：true
解释：”.“ 表示可匹配零个或多个（’*’）任意字符（’.’）。

代码详解

这道题是(hard)，比较难的一道题。

/*
方法一：动态规划（官方算法，很巧妙，也很复杂） ***困难难度***
    这道题难度为困难，题目中的匹配是一个逐步匹配的过程：我们每次从字符串p中取出一个字符或
    或字符+星号的组合，并在s中进行匹配。对于p中一个字符而言，只能在s中匹配一个字符，匹配
    方法具有唯一性；对于p中字符+星号的组合，可以在s中匹配任意个相同字符。

    用f[i][j]表示s的前i个字符和p中前j个字符是否能够匹配，在进行状态转移时，考虑p的第j个
    字符的匹配情况：
        如果p的第j个字符是字母或是 . 那么s中必须匹配一个相同的字母，判断函数如下
            当s[i] = p[j]时， f[i][j] = f[i - 1][j - 1];
            当s[i] != p[j]时，f[i][j] = false;
        如果p[j]是“ * ”星号，考虑字符 + 星号的组合在匹配过程中本质上只会出现两种情况
            匹配s末尾的一个字符，将这个字符丢掉后，依然可以匹配
            不匹配字符，直接将组合丢掉，不再进行匹配  判断函数如下
            当s[i] = p[j - 1]时，f[i][j] = f[i - 1][j] or f[i][j - 2]
            当s[i] != p[j - 1]时，f[i][j] = f[i][j - 2]
            **多思考这段代码的逻辑**
    
    细节：动态规划的边界值f[0][0] = true，因为两个空字符串可以相互匹配，最终的答案为f[m][n]
          m，n分别是字符串s，p的长度
*/
bool isMatch(string s, string p){
        int m = s.length();
        int n = p.length();

        auto matchs = [&](int i, int j){    //c++11的lambda表达式，匿名函数，速度更快，写法简洁
            if(i == 0){
                return false;       //s空字符串与任何字母都不匹配
            }
            if(p[j - 1] == '.'){
                return true;
            }
            return s[i - 1] == p[j - 1];
        };

        vector<vector<int>> f(m + 1, vector<int>(n + 1));
        f[0][0] = true;
        for(int i = 0; i <= m; i++){
            for(int j = 1; j <= n; j++){
                if(p[j - 1] == '*'){
                    f[i][j] |= f[i][j - 2];  //因为每次出现*时，都能保证*前面有可以匹配的字符，不用担心j-2会溢出
                    if(matchs(i, j - 1)){
                        f[i][j] |= f[i - 1][j]; 
                    }
                }
                else{
                    if(matchs(i, j)){
                        f[i][j] |= f[i - 1][j - 1];
                    }
                }
            }
        }
        cout << f[0][1] << endl;
        return f[m][n];
    }